3. Mathematische Ausdrücke
Die kürzeste und präziseste Darstellung eines Zusammenhanges, eines Prozesses oder einer Struktur liefert der mathematische Ausdruck. Der Umgang mit ihm erfordert Übung und Erfahrung.
Gleichungen
Gleichungen sind Aussagen, in denen die Gleichheit zweier Werte oder Terme durch das Gleichheitszeichen ausgedrückt wird. Sie stellen den quantitativen Zusammenhang von variablen und konstanten Größen in mathematischer Form her und sind wichtige Beschreibungs- und Berechnungsinstrumente der Technologie
Das Verhalten der Spannung U und der Stromstärke I an einem Widerstand R ist proportional.
Die Gleichung beschreibt dieses Verhalten. Mit ihr kann der Wert des Widerstandes, eines Spannungsabfalls oder einer Stromstärke berechnet werden.
R = U/I
Diese Gleichung drückt aus, dass die elektrische Leistung P eines Widerstandes der Spannung U und der Stromstärke I proportional ist. Die Leistung ist das Produkt beider Größen.
P = U · I
Die Arbeit W, die ein elektrischer Widerstand verrichtet, ist der Leistung P und der Zeit t proportional. Die Arbeit ist das Produkt beider Größen.
W = P · t → W = U · I · t
Diagramme
Ein Diagramm ist eine grafische Darstellung, die Zusammenhänge von Daten und Sachverhalten abbildet. Die Anwendung ist sehr vielfältig und reicht von bildhaften Elementen bis zu abstrakten Gebilden.
Diagramme sind oft codiert. Das bedeutet, dass nur mithilfe von Vorwissen ein Diagramm analysiert und verstanden werden kann.
Liniendiagramme
Beispiel 1: Beschreibung des Verhaltens eines elektronischen Bauelements
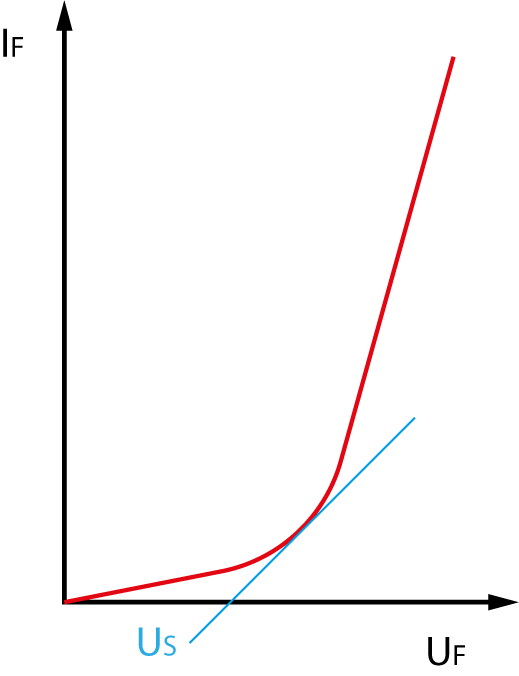
Der Kennlinie einer Diode können den folgenden Informationen entnommen werden:
Mit wachsender Spannung UF nimmt die Stromstärke IF zu. Charakteristisch ist, dass die Zunahme der Stromstärke exponentiell verläuft.
Der im Diagramm nicht erkennbare Grund dafür ist, dass bei Überschreiten der Schleusenspannung US sich der Widerstand der Diode zunehmend verringert.
Dieses Beispiel enthält keine quantitativen Informationen.
Beispiel 2: Beschreibung eines Vorgangs
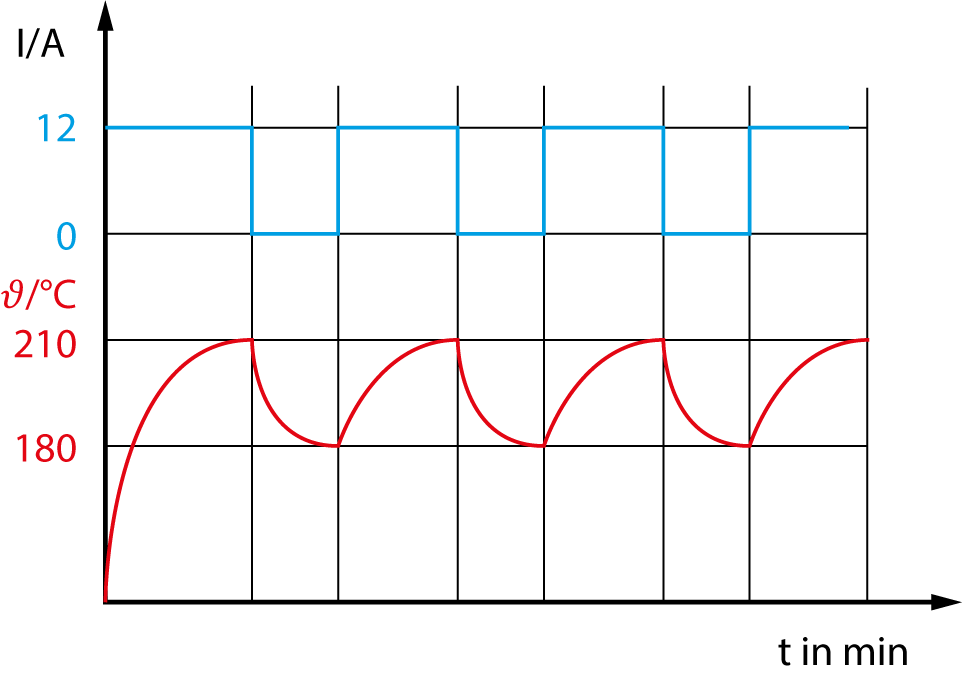
Das Diagramm zeigt das Regelverhalten eines 2-Punkt-Reglers am Beispiel eines Bügeleisens.
Beim Einschalten erhöht sich die Temperatur bis auf 210°C. Dann schaltet der Regler den Strom aus. Die Temperatur verringert sich beim Bügeln bis auf 180°C, und der Regler schaltet den Strom wieder ein, usw.
Das Diagramm enthält als quantitative Informationen die Zeit, Temperaturen und die Stromstärken.
Flussdiagramme
Flussdiagramme werden zur Abbildung von Prozessen mit Erhaltungsgrößen verwendet. Energie, Masse und elektrische Ladung sind Erhaltungsgrößen. Für sie gilt der Erhaltungssatz.
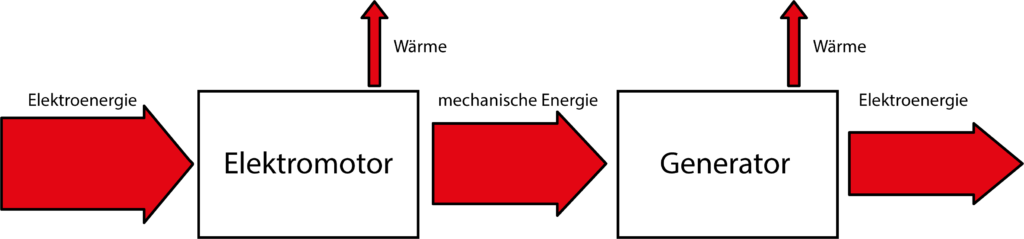
Beispiel 3: Energieflussdiagramm
Das Beispiel zeigt die Energieflüsse einer elektrischen Maschine, die einmal als Motor und einmal als Generator betrieben wird.
Unabhängig von der Betriebsart ist die zugeführte Energie immer gleich groß der Summe aus der abgegebenen nützlichen Energie plus der Wärmeverluste.
Vektordiagramme
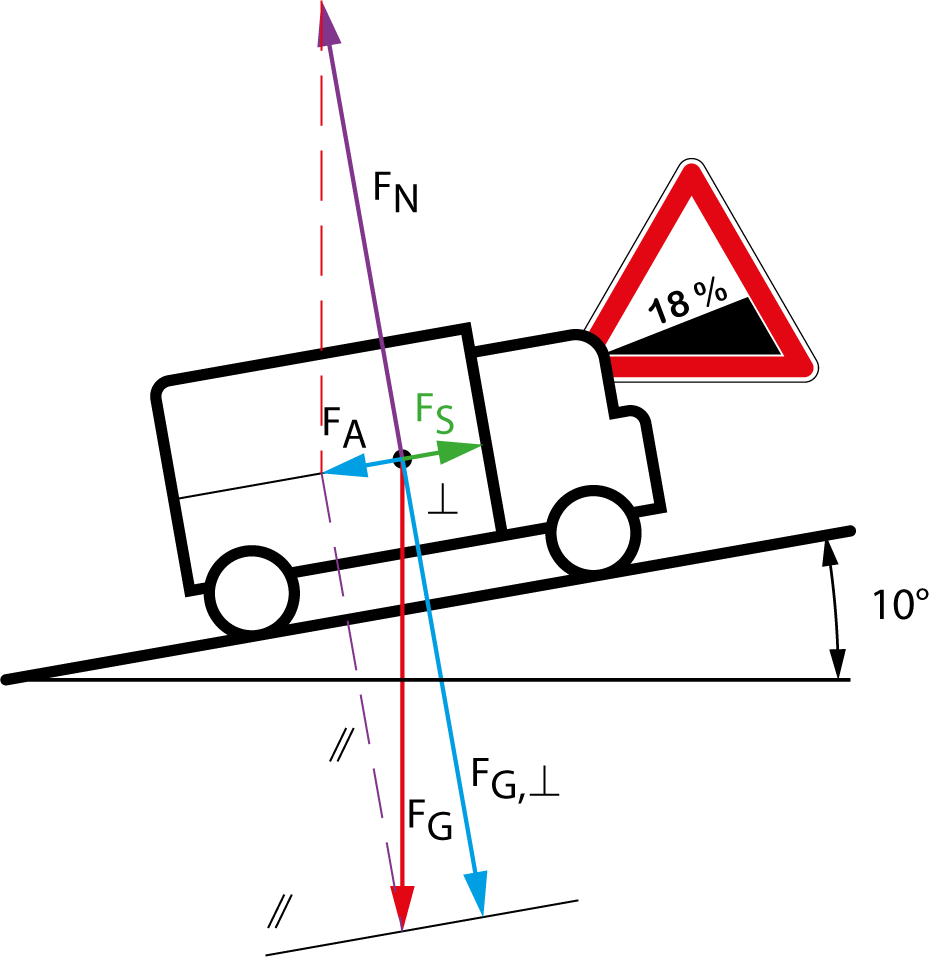
Vektordiagramme werden verwendet, um z.B. Kräfte und Geschwindigkeiten graphisch darzustellen. Sie sind die Grundlage für Berechnungen.
Beispiel 4: Bildung einer Summenkraft aus zwei Vektoren
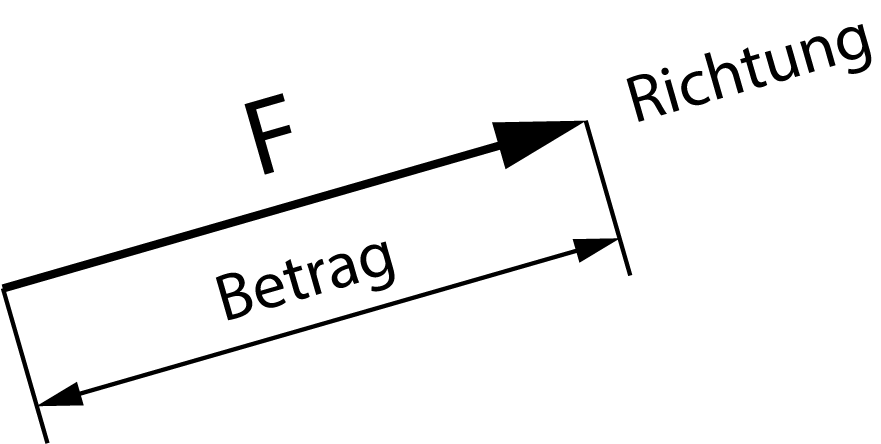
Kräfte werden mit Vektoren abgebildet.
Vektoren haben einen Betrag und eine Richtung. Sie können zusammengesetzt werden, sodass z. B. Summenvektoren entstehen. Diese zeigen im Beispiel die resultierende Richtung und den Betrag der Summenkraft an.